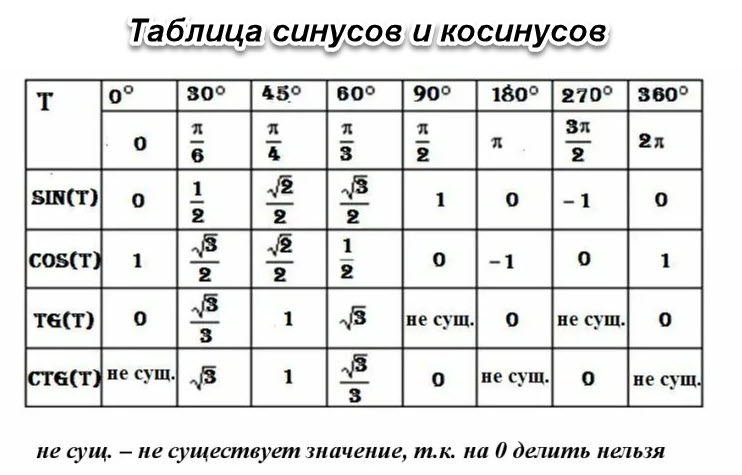
Таблица синусов и косинусов
Таблица косинусов — значения косинусов углов записаны в таблицу от 0° до 360°.
Используя таблицу косинусов вы сможете провести расчеты даже если под рукой не окажется инженерного калькулятора. Чтобы найти значение косинуса нужного вам угла достаточно использовать таблицу косинусов углов.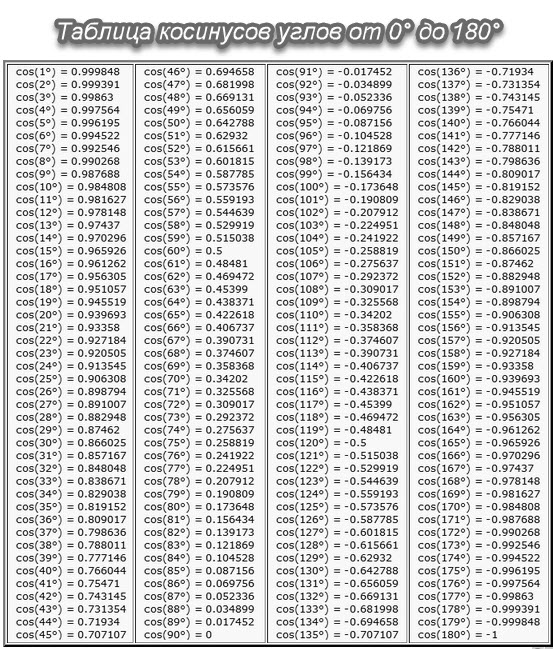
Таблица косинусов — с таблицей синусов изучается в самом начале тригонометрии. Без понимания таблицы косинусов углов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. Является по сути лишь показателями отношения различных сторон прямоугольного треугольника друг к другу, результат которых сводится к решений прямоугольных треугольников.
Одной из основных тригонометрических функций является косинус острого угла. В данной таблице косинусов углов вы сможете найти любое значение косинуса.
Таблица синусов углов в градусах: значения и применение
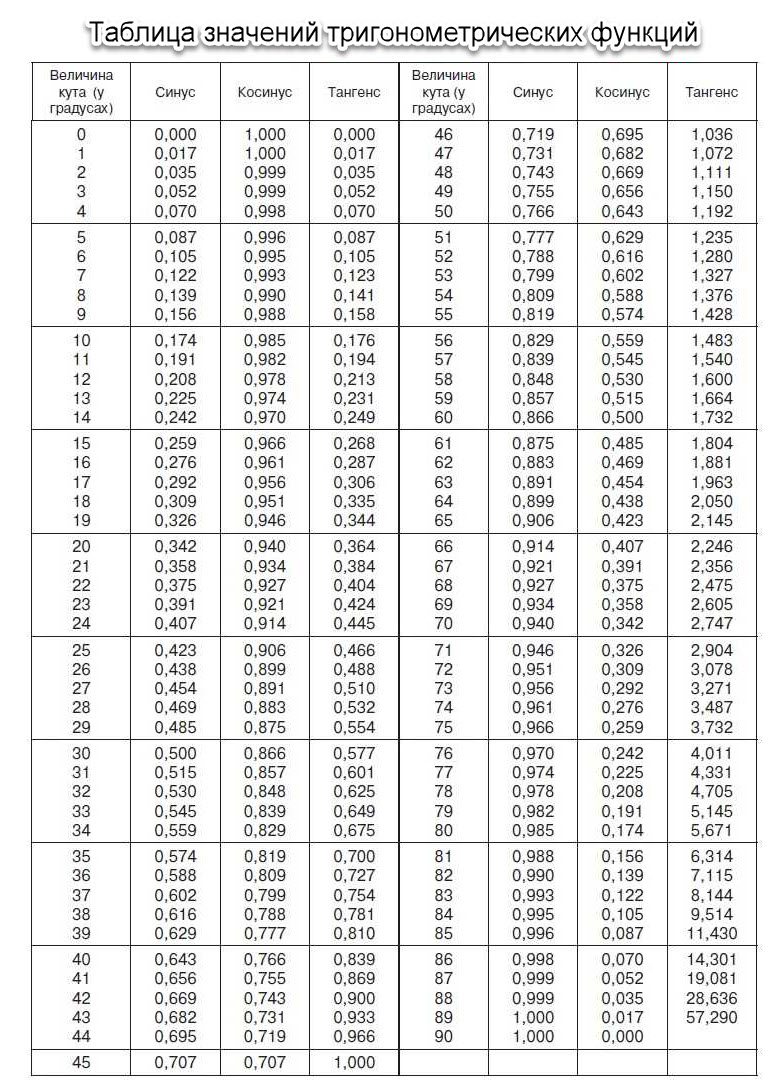
Синусы углов: как легко до них добраться?
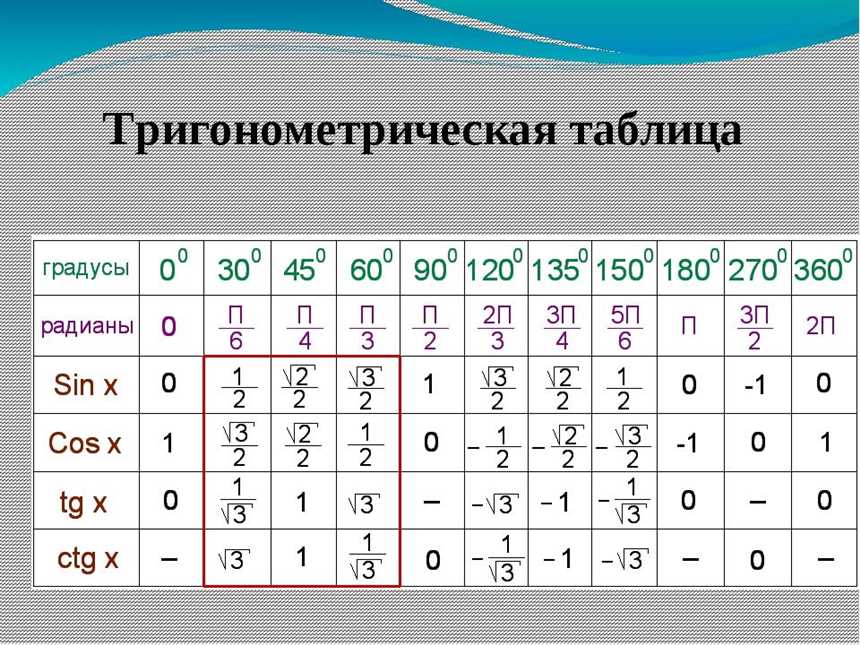
Синус угла — это функция, которая выражает отношение противоположной стороны треугольника к его гипотенузе. Синус угла можно выразить в градусах или радианах, но в данной статье мы сосредоточимся на градусах. Зная значения синусов основных углов, мы можем легко вычислить синус любого другого угла.
Периодичность и запоминание значений синусов углов
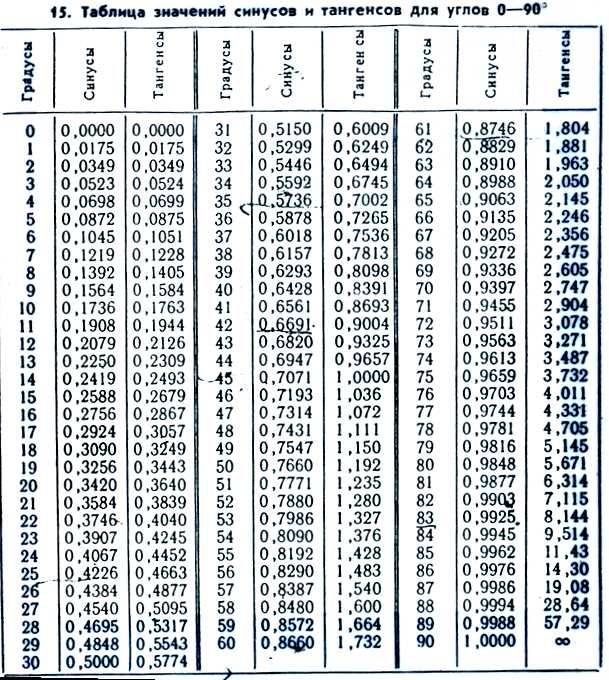
Значения синусов углов имеют периодичность, повторяясь с определенным шагом. Запомнить значения синусов углов от 0° до 180° можно с помощью таблицы:
| Угол (градусы) | Значение синуса |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.707 |
| 60° | 0.866 |
| 90° | 1 |
| 180° | 0 |
Также для удобства запоминания можно использовать вариант: «получай 0, получай 1 и корень из двух под наклоном». Эта фраза поможет вам быстро вспомнить значения синусов для основных углов.
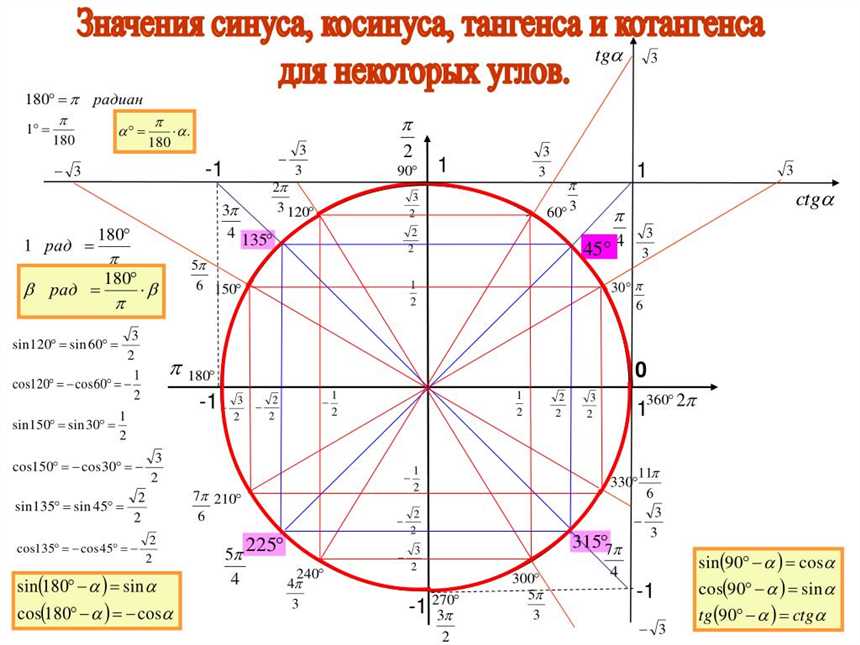
Значения синусов углов от 0° до 360°
Если в таблице представлены значения синусов углов от 0° до 180°, как же узнать значения синусов для углов от 180° до 360°? Для этого можно использовать следующую таблицу:
| Угол (градусы) | Значение синуса |
|---|---|
| 180° | 0 |
| 210° | -0.5 |
| 225° | -0.707 |
| 240° | -0.866 |
| 270° | -1 |
| 360° | 0 |
Теперь для углов от 180° до 360° можно использовать полученные значения синусов.
Применение значений синусов углов
Зная значения синусов углов, мы можем их использовать в различных областях. Например:
- При решении задач физики, где необходимо учесть силу трения, давление в жидкостях и другие физические явления;
- При вычислении координат точек на графике;
- При моделировании и анализе процессов в инженерном дизайне;
- В тригонометрии для решения уравнений и построения графиков.
Используйте таблицу синусов углов для упрощения вычислений и решения различных задач!
Синус угла: таблица синусов
Синус угла является одной из основных тригонометрических функций, описывающих соотношение между сторонами и углами в прямоугольном треугольнике. Он определяется как отношение противолежащего катета к гипотенузе.
Синус угла измеряется в градусах или радианах и принимает значения от -1 до 1. Существует множество значений синуса для различных углов, но наиболее удобным способом запомнить значения синусов для разных углов является использование таблицы синусов.
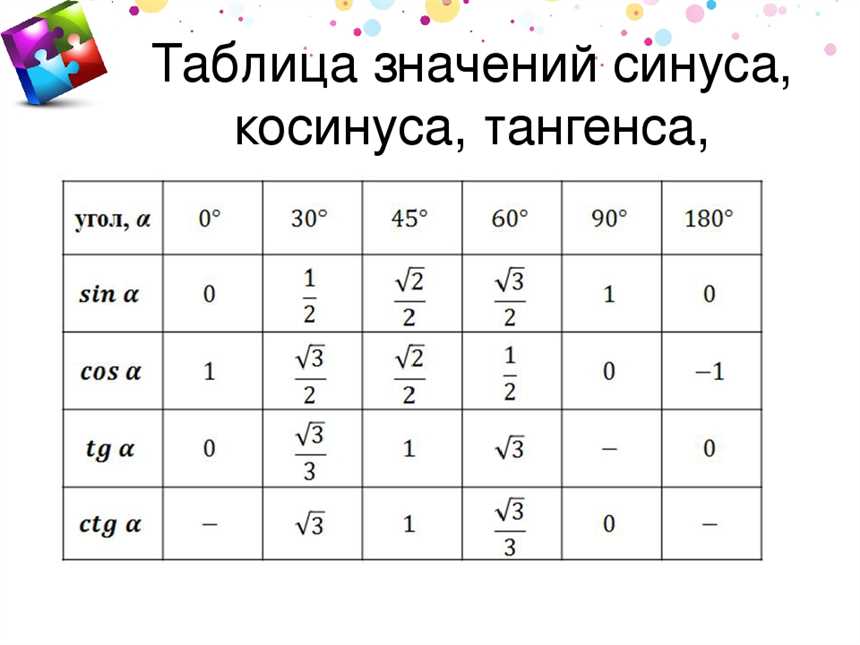
Таблица синусов углов в градусах:
| Угол (градусы) | Синус угла |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.707 |
| 60° | 0.866 |
| 90° | 1 |
Таблица синусов позволяет легко узнать значения синуса для углов от 0° до 90°. Она может быть использована как справочник при работе с углами и тригонометрическими функциями. Кроме этого, таблица синусов может быть использована как помощник для запоминания значений синуса угла в виде чисел.
Для углов, превышающих 90°, таблица синусов может быть использована с использованием периодичности значений синуса. Например, синус угла 181° будет иметь такое же значение, как и синус угла 1°. Аналогично, синус угла 181° будет иметь такое же значение, как и синус угла 359°.
Зная значения синусов для основных углов и используя периодичность, можно легко определить значения синуса для любого угла в пределах 0°-360°.
Калькулятор и таблица синуса и косинуса: значения с шагом в градусах и радианах
Синус и косинус — основные тригонометрические функции, широко используемые в математике, физике, инженерном и научном моделировании. Они связаны с геометрией и позволяют рассчитывать стороны и углы треугольника, особенно между прямоугольным треугольником и острым треугольником. Для подробной работы с этими функциями мы можем использовать таблицу значений синуса и косинуса.
Таблица значений синуса и косинуса представляет собой список углов, начиная от 0° и двигаясь с шагом 1° или другим углом, до 180° или более. Значения синуса и косинуса можно использовать для решения задач, связанных с тригонометрическими углами и прямоугольными треугольниками. В таблице также указаны значения синуса и косинуса в радианах.
Например, если нам нужно найти косинус угла 30°, мы можем взглянуть на таблицу значений и обнаружить, что косинус 30° равен 0.866. Аналогично, если мы нуждаемся в значении синуса угла 60°, то значение 0.866 также находится в таблице.
Таблица значений синуса и косинуса позволяет легко находить значения этих функций для разных углов. Она полезна не только для математических расчетов, но и для решения инженерных задач, физических задач и для проведения различных научных исследований.